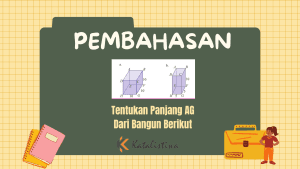
Tentukan Panjang AG Dari Bangun Berikut

July 12, 2025 Pendidikan 91 Views

Selamat datang di Katalistiwa, blog untuk berdiskusi seputar pembahasan soal pelajaran dari Perguruan Tinggi, SLTA, SMP dan SD. Kali ini Katalistiwa akan membahas sebuah Soal yang banyak ditanyakan di Ujian Sekolah, Pertanyaannya adalah : Tentukan Panjang AG Dari Bangun Berikut

Tentukan Panjang AG Dari Bangun Berikut

Jawab :

Rumus :

Diagonal bidang kubus = s√2
Diagonal ruang kubus = s√3

Diagnal bidang balok = $\\sqrt{ p^{2}+l^{2} }$
Diagonal ruang balok = $\\sqrt{ p^{2}+l^{2} + t^{2}}$

Penjelasan tentang panjang AG dari Bangun Balok dan Kubus

Panjang AG pada kubus dan balok merupakan diagonal ruang.

No. a. Kubus

AG² =HG² + FG² +BF²
AG² =10² + 10² + 10²
AG² = 10² × 3
AG = $\\sqrt{ 10^{2}\\times 3 }$
AG = 10√3

Jadi panjang AG pada kubus adalah 10√3

No. b. Balok

AG²= HG² + FG² + BF²

AG²=5² + 5² + 10²
AG² = 25 + 25 + 100
AG² = 150
AG = √150
AG = $\\sqrt{25 \\times 6}$
AG = 5√6

Jadi panjang AG pada balok adalah 5√6

Detail Soal

Kelas : 8
Mapel : Matematika
Kategori : Bab 5 – Teorema Pythagoras
Kata kunci : balok, diagonal ruang
Kelas 8 Matematika

Bab 5 – Teorema Pythagoras

Inilah Pembahasan yang sudah kami rangkum oleh Tim Katalistiwa.id dari berbagai sumber belajar. Semoga pembahasan ini bermanfaat, jangan lupa jika mempunyai jawaban lain kalian bisa menghubungi admin. Terimakasih

Post Views: 137

Recommendation:

Berapa Luas Permukaan Bangun Diatas? Hitung Disini! Jika Anda penasaran untuk mengetahui berapa luas permukaan bangun di atas, maka Anda telah datang ke tempat yang tepat! Di artikel ini, kami akan memberikan penjelasan lengkap serta rumus untuk menghitung luas permukaan bangun tersebut. Tak perlu khawatir, pembahasan akan…
Bangun Kubus Adalah Bangun Yang Sisi Sisinya Berbentuk Halo anak-anak! Pada kesempatan ini, kita akan menjelajahi tentang bangun kubus. Apakah kalian tahu apa itu bangun kubus? Bangun kubus adalah salah satu bentuk bangun ruang yang memiliki sisi-sisi yang berbentuk persegi. Jadi, setiap sisi pada bangun kubus ini adalah…
Apa yang Dimaksud dengan Daerah Tempat Penulisan… Kamu pasti pernah mendengar tentang "Daerah Tempat Penulisan Rumus Excel", bukan? Mungkin bagi sebagian orang, itu terdengar seperti daerah misterius yang hanya diketahui oleh para ahli matematika atau programmer. Tetapi sebenarnya, daerah ini merupakan salah satu fitur yang sangat berguna…
Rumus Mencari Volume Balok dan Luas Balok Selamat datang di Katalistiwa, blog untuk berdiskusi seputar pembahasan soal pelajaran dari Perguruan Tinggi, SLTA, SMP dan SD. Kali ini Katalistiwa akan membahas sebuah Soal yang banyak di tanyakan di Ujian Sekolah, Pertanyaannya adalah : Rumus Mencari Volume Balok dan…
Mengapa Volume Termasuk Besaran Turunan? Hai, sahabat! Apakah kamu pernah berpikir mengapa volume termasuk besaran turunan? Nah, dalam artikel kali ini, kita akan menjelajahi konsep yang menarik ini. Bersiaplah untuk dipahami dan dijawab pertanyaan-pertanyaanmu mengenai volume. Jadi, ayo mulai dan mari kita belajar bersama! Mengapa…
Sebutkan Jaring Jaring Kubus Selamat datang di Katalistiwa, blog untuk berdiskusi seputar pembahasan soal pelajaran dari Perguruan Tinggi, SLTA, SMP dan SD. Kali ini Katalistiwa akan membahas sebuah Soal yang banyak di tanyakan di Ujian Sekolah, Pertanyaannya adalah : Sebutkan Jaring Jaring Kubus …